Profile
In the area of teaching and research we want to build a bridge between theory and practice. Mathematical methods help us to investigate real technical systems. These are represented as numerical simulations and influenced by control algorithms, such as model predictive control. The results of our investigations are finally applied to the real system. From hardware-oriented programming using C/C++ to numerical simulations using MATLAB/Simulink or Julia, we work with different software to implement our projects. Our focus is mainly in the following areas. Our research topics are described on the page of the Research Group Control and Process Engineering presented.
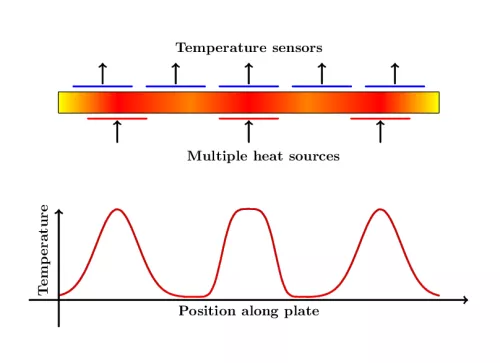
Thermal process technology
Temperature plays a decisive role in many technological processes. Be it the air conditioning of buildings, the cooling of motors or high performance computers, or the optimal heating for the production of plastics - the correct heat supply and removal are crucial. In our group we deal with the control of heat conduction problems under the influence of multiple actuators. Here, the control algorithms must decide not only how much heat to apply, but also at what point. Typical fields of application are industrial baking processes, for example in the semiconductor industry.
Scientific Machine Learning
Modern machine learning techniques have an important impact not only on IT services such as search engines and social networks. Many scientific methods also rely on data-driven modeling to study complex systems. These complex systems are often too large to be described in detail. Therefore, we as developers and scientists use so-called grey-box models, which allow us to approximate the theoretical model to the real one with the help of large data sets when we only have partial knowledge of systems. Examples are vehicle dynamics, where every component has an influence on the ride, or chemical reactions, where a huge number of particles or reactants interact.
See also: SciML
Embedded systems
From household electronics to industrial control systems, microelectronic circuits can be found as embedded systems in almost every area of life. These are often used for measuring and processing data, for example lighting control in buildings. Since commercial industrial control systems are often less flexible in their field of application and usually more cost-intensive than single-board computers, we are testing their application in small industrial environments. Process engineering, electrical and mechanical systems serve us as underlying hardware, which is controlled by means of embedded systems.
Projects and theses
We offer projects and theses related to our research areas: Thermal Process Engineering, Scientific Machine Learning and Embedded Systems. Thematically, interested students can choose between software projects with solid theoretical foundations or hardware-related development for the laboratory including practical experiments and their evaluation.
Software development
We develop mathematical models and controls for complex dynamical systems and implement them in modern programming languages like Julia, MATLAB/Simulink or C/C++. Projects and theses in the following areas are offered:
- Scientific Machine Learning using Neural ODE and Universal ODE,
- Optimal Control and Model Predictive Control with CasADi or JuMP and
- Discretized thermal problems as high-dimensional systems.
Hardware related development
We are working on the transformation of proprietary hardware and software to free and open solutions such as Raspberry Pi or Arduino. The projects we offer include all areas of control and systems engineering such as
- the design and construction of hardware
- the modeling and system identification of plants and
- the implementation of controls and user interfaces.
For this we offer the following experiments as basic hardware:
- electrical and mechanical oscillators
- hydraulic models (water tank, heeling control) and
- inverse pendulum.
Downloads
- Topics for theses and projects in the field of control engineering, modeling and simulation.
Seminar
In the Embedded Control Seminar and Lab students investigate a topic of current research or development in control engineering, implement an application example using simulation tools, adapt the method for use in embedded systems, and present the results to an audience. Topics from all areas of control engineering are offered, such as the optimal control, nonlinear control or control using machine learning and from related areas such as Mathematical Optimization, Numerical Mathematics or Computer Science.
| A |
|
| B |
|
| A |
|
| B |
|
|
Teaching
We offer courses in the area of control engineering and embedded systems.
List of courses
| Microcontroller | Winter / Summer | Lecture and practical course | Moodle course |
| Control Engineering | Winter / Summer | Lecture and practical course | Moodle course |
| Advanced Control Systems: Digital Control | Summer only | Lecture and lab | Moodle course |
| Embedded Control | Winter only | Seminar and practical course | Moodle course |
| Embedded GUI | Summer only | Lecture and lab | Moodle course |
| Numerical Methods | Moodle course | ||
| Tutorial Control Engineering (optional) | Winter / Summer | Moodle course |
Control engineering
This course provides an introduction to linear dynamical systems in the continuous and discrete time and frequency domains. The modeling of ordinary differential equations and transfer functions, and the design of control systems using heuristic, algebraic, and graphical methods are covered.
Contents
- Modeling of dynamical systems in time and frequency domain
- Laplace transformation
- Transfer functions
- Block diagrams
- Analysis of open and closed loop linear control systems
- Proportional, integral and differential (PID) behavior
- Bounded-input-bounded-output (BIBO) stability
- Bode and Nyquist diagrams
- Control design using algebraic, graphical and heuristic methods
- Routh-Hurwitz criterion
- Nyquist criterion
- Design of root locus curves
- The methods of Ziegler-Nichols and Naslin
- Digital control systems in the frequency domain
- Z-transformation
- Zero-Order Hold
- Bilinear transformation (Tustin method)
- Jury's stability criterion
- Dead-beat controller
Advanced Control Systems
Modern complex dynamical systems are modeled, simulated and controlled in the time domain as will be presented in this course. In particular, common methods in the state space for the analysis and control of linear time-invariant systems are discussed. In addition, modeling and control of nonlinear systems will be introduced.
Contents
- Modeling of dynamical systems in state space
- Laplace transformation
- Eigenvalues and eigenvectors
- Stability of linear time-invariant systems
- Design of feedback systems
- Controllability
- State feedback
- Ackermann's method
- MIMO systems using eigenvalue decomposition
- Design of state observers
- Observability
- State observer according to Luenberger
- Separation of controller and observer
- Introduction to optimal control
- Linear-Quadratic Control
- Nonlinear systems and methods of discretization
- Zero-Order Hold
- Lyapunov Stability
- Van der Pol Oscillator
- Introduction to nonlinear control systems
- Sliding-Mode Control
- Nonlinear model predictive control
Downloads
- MATLAB-Einführung Skript
- V1 Frequenzgang und Übergangsfunktion Skript
- V2 Drehzahl- und Winkellageregelung Skript
- V3 Wurzelortskurven Skript
- V4 Heizungsregelung Skript
Contact & People
General contact details
| Phone | |
|---|---|
| Room | H240 |
| On campus |
Building H (main building)
Doggenriedstrasse 70
88250 Weingarten |
| Postal address |
RWU Hochschule Ravensburg-Weingarten University of Applied Sciences Control and Process Engineering P.O. Box 30 22
88216 Weingarten Germany |
Laboratory Team


- Building H (main building)
- Room H 062 / H 063 / H240
